最大流从入门到精通

Shq 2018-08-06 17:35:28

By - Shq

网络流是个十分常用的方法，拥有很多用途

之前的讲解太草率了qwq，这一篇我们来好好介绍一下网络流

网络流 - 网络

网络是一张有向图，有且仅有 一个汇点和一个源点

我们来举一个 简单易懂 的栗子:

你是一个工厂老板

你有一座超大的工厂，大到它可以制造任意多的货物。但是众所周知，工厂是不会建在市区的。

从工厂到销售处之间有若干车站，车站间有若干车次。每个车次有一个起点、一个终点（单向的），还有一个容量，指你最多可以利用个车次载多少货物。最大化你从工厂运到销售处的货物量

这是一个很显然的栗子

栗子中你的工厂就是源点，销售处(我们规定只有一个销售处)就是汇点

画一个简单的图：

网络流

By Shq + GeoGebra

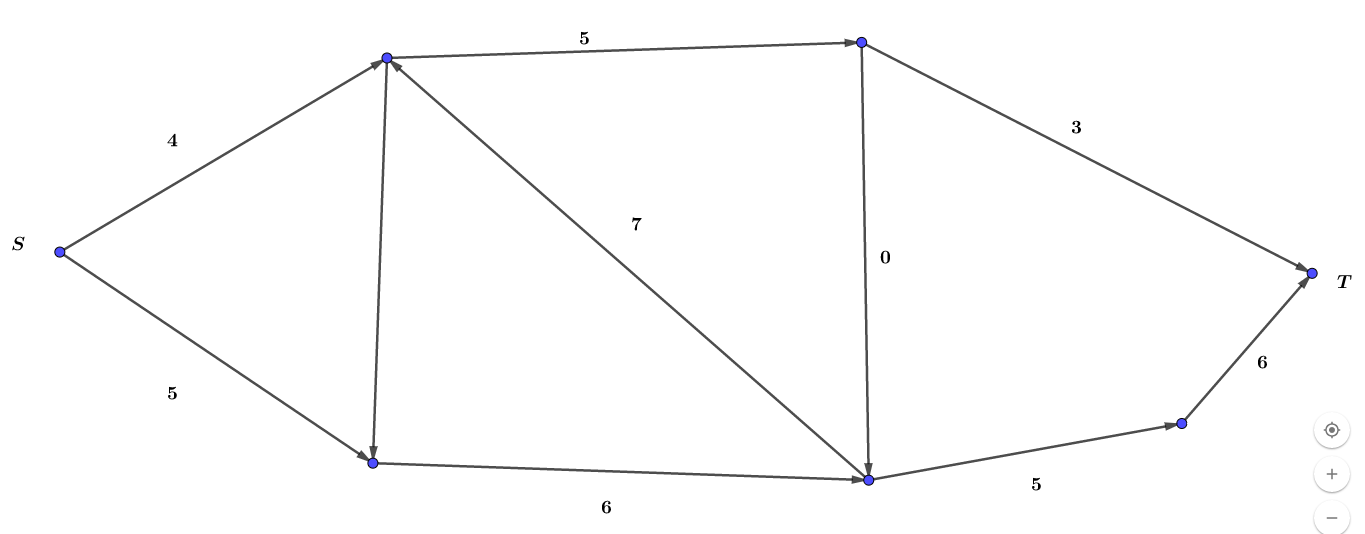
图中的代表源点，代表汇点

每条边表明了流量

我们将⼀个合法解称作⼀个流，⼀条边被经过的次数称作其流量；

最终运输的货物总数称作整个流的流量

容量限制：每条边被经过的次数不得超过它的容量每条边的流量不超过其流量

流量平衡：流由若⼲从源点到汇点的路径组成除源点和汇点外，对于每个点，流⼊它的流量和等于从它流出的流量和

最⼤化货物量最⼤化整个流的流量最⼤化从源点流出的流量

网络的一些性质

网络流的性质有很多，这里先介绍一些常用的性质

容量：表示一条有向边的最大允许的流量
流量：表示一条有向边总容量中已被占用的流量
剩余容量：即，表示当前时刻某条有向边总流量中未被占用的部分
反向边：原图中每一条有向边在残量网络中都有对应的反向边，反向边的容量为，容量的变化与原边相反；『反向边』的概念是相对的，即一条边的反向边的反向边是它本身
残量网络：在原图的基础之上，添加每条边对应的反向边，并储存每条边的当前流量。残量网络会在算法进行的过程中被修改
增广路（）：残量网络中从源点到汇点的一条路径，增广路上所有边中最小的剩余容量为增广流量
增广（）：在残量网络中寻找一条增广路，并将增广路上所有边的流量加上增广流量的过程
层次：表示节点在层次图中与源点的距离
层次图：在原残量网络中按照每个节点的层次来分层，只保留相邻两层的节点的图，满载（即流量等于容量）的边不存在于层次图中

这里当然有一些 dinic 的内容，这里看看就好啦

最大流

现在我们想一种状况

你工厂生产的产品十分畅销，销售部经常卖光，你每次都要制造产品，再运过去很麻烦。于是，你制造了顿货物，但是由于每条边都有一个流量限制，到达销售部的货物肯定不会是你发出货物的数量

你开始思考，我们最多生产多少顿货物，可以让销售部收到同样多的货物

这个货物的数量就是这个网络的最大流

我们先看一种 看似正确的 解法

Shq 蒟蒻解法:

找⼀条任意的路径并流过去，直到找不到一条合法的路径qwq

我们来考虑一下反例：

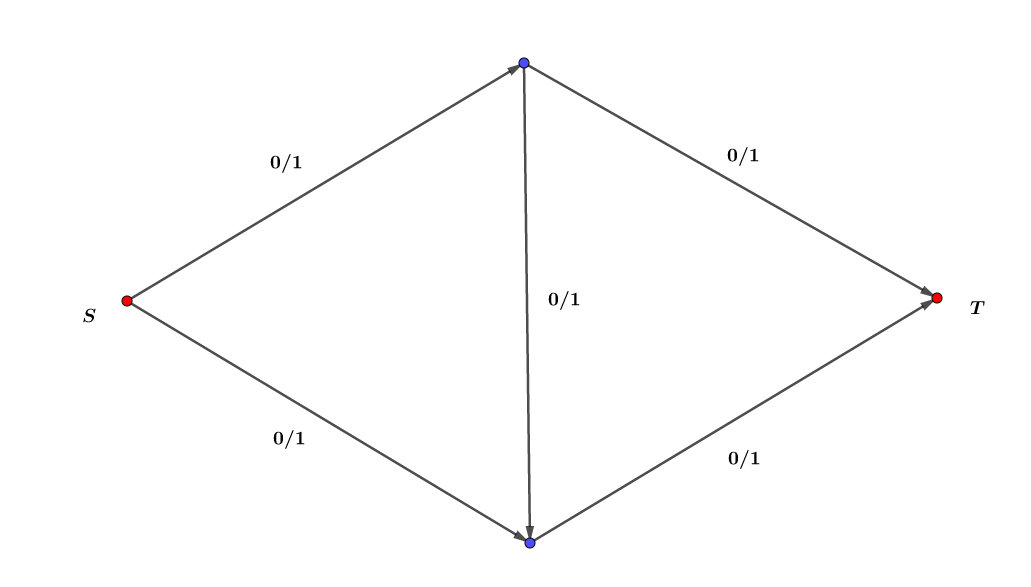
我们要求这个网络的最大流

肉眼都能看出这个网络的最大流是

我们沿用刚刚的思路，假如我们看到了这样一条路径:

反例2

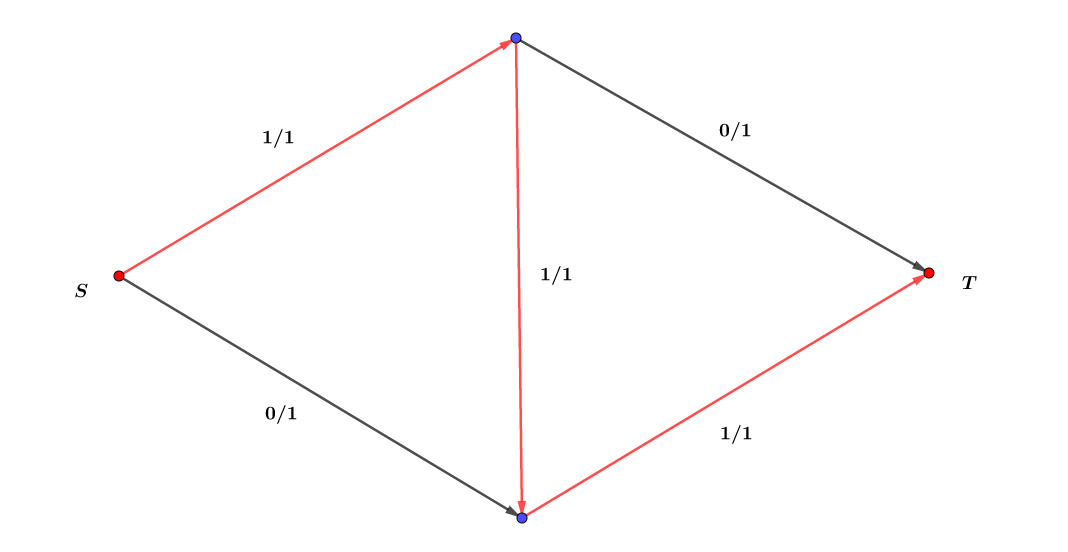
这个算法会有一个错误的答案

我们想想如何改进这个算法，首先我们看一看我们失败的原因

我们失败的原因是我们选择了一条错误的路径

那个.....有什么办法可以反悔呢？

如何做到 可以反悔 呢

每次我们找到了道路后，我们可以建一条 反向边 ,容量为这条边的容量

减少⼀条边上的流量，相当于反向流过来的流量

这个还是⽐较显然的。假设你把⼀些货物从地运到地，后来你发现运错了，那就再运回来就⾏了qwq

定义: ⼀条边的残量，是指它还能流多少流量（即容量减去当前流量）

反向边

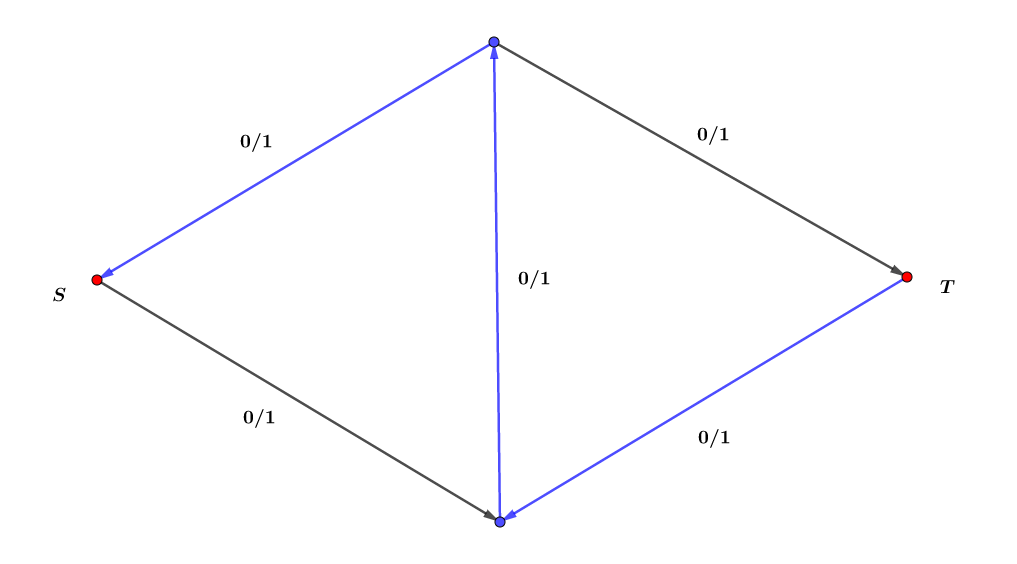
这样，我们就又能发现一条道路！

新的道路

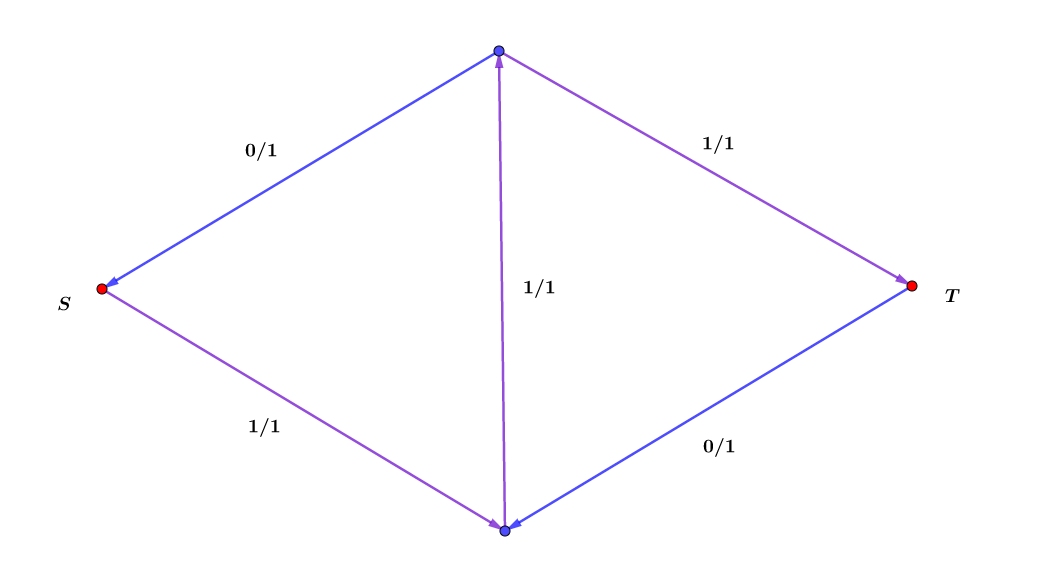
现在这个网络的最大流就显然是了

这条路径就叫做增广路 ()，当然，增广路不止这一条qwq

最大流 - 算法

我们来给这个简单显然的方法整理一下:

这明显就是贪心啊qwq

我们来尝试证明一下：

首先，对于算法求出的流为 , 对应的残余网络中从可达的顶点集合为，因为对应的残余网络中不存在从的路径了

那么显然，在残余网络中，任意一条从中的边流量 ,任意一条从反向弧，这个一定是满足，如果不满足，那么集合还可以扩充顶点，与前提矛盾。因此，的割的容量等于流的大小。则可以证明裸的増广路算法是正确的

最小割

我们刚刚在证明的时候出现了一个十分神奇的 割 字，那么他到底是啥呢？

所谓图的割，指的是某个顶点集合属于，从出发的所有边的集合成为割 ,这些边的容量和被称为割的容量，如果有源点属于，汇点属于，则称之为割，如果将割的所有边都在原图中去掉，则不再有的路径

我们还是举个栗子：

又双叒叕是这个图：

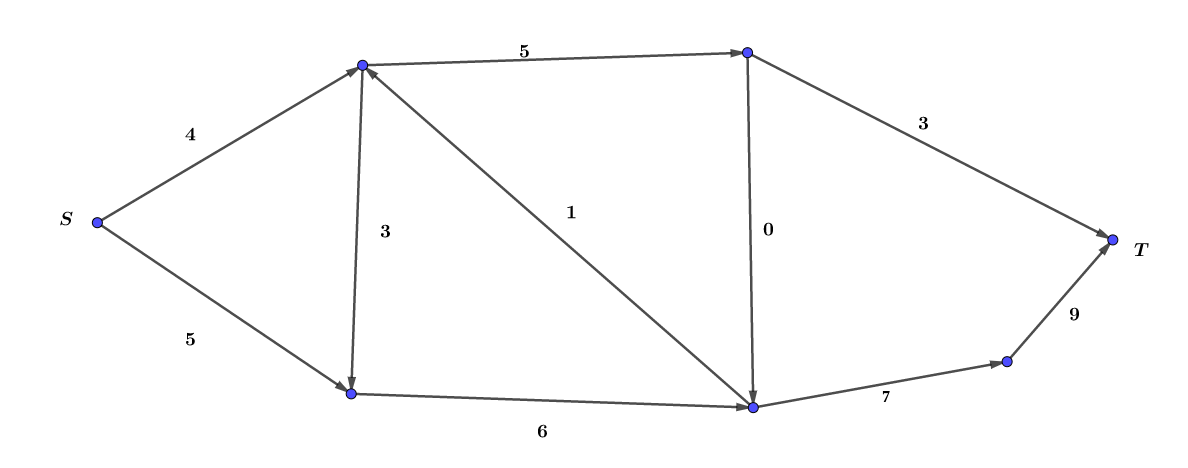
你和某家工厂的老板有仇

你想破坏他的工厂销售，但是明显的，你破坏工厂和销售部明显是不明智的，你可以破坏他工厂的运输即可qwq

你需要找到一些道路，使从工厂到销售部没有道路链接，但是你并非想花费很大力气，你想找到一些花费力气最小的道路，选出⼀些边的集合，使得删除它们之后从源点⽆法到达汇点，那么这个集合就叫做⼀个割

这些边的容量之和称作这个割的容量

我们任取一个割，我们发现它始终好像比最大流大的流量？

从源点到汇点的每条路径都会经过割上的⾄少⼀条边。割掉这些边之后，把源点能到达的点放到左边，不能到达的放到右边。显然源点到汇点的流量不会超过从左边⾛向右边的次数，⽽这⼜不会超过从左边到右边的边的容量之和。

直观⼀点，假设你是在⻋装着货物的时候炸掉了它。

每个货物你⾄少付出的代价炸掉（流量⼩于容量的时候你要付出⽐货物数更多的代价），所以你炸的代价 不会⼩于 货物数

对于一个网络

我们可以直观的看出来从的最大流是

它的最小割为

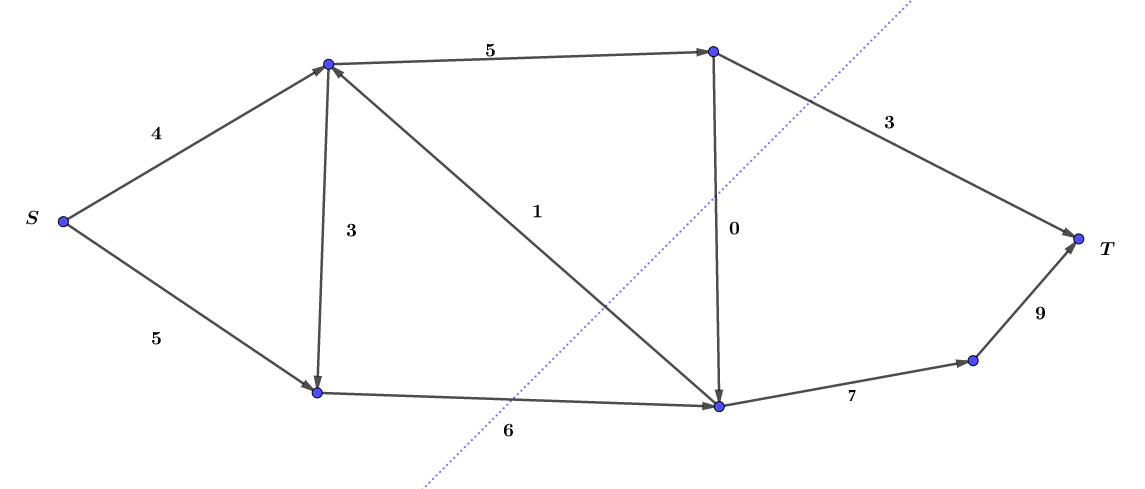
网络的最小割

经过我们的实验发现，最小割的容量等于最大流的流量

这个和最小割最大流有关，我们就干脆命名为 最小割最大流定理

这意味着⼀个惊⼈的事实：你能够仅付出和货物数相同的代价，就把你的仇⼈的财路炸断！

这自然是看起来很玄学的，我们想想为什么这个是成立的

最小割最大流定理

求证：最小割的容量等于最大流的流量，并且能够正确地求出来它

考虑算法结束时，残量⽹络上没有了增⼴路。那么我们假设这时候，从源点经过残量⽹络能到达的点组成的集合为，不能到达的点为。显然汇点在⾥，并且残量⽹络上没有从到的边。

可以发现以下事实成⽴：

到的边流量为。如果流量不为那么应该存在⼀条从到的反向边，于是⽭盾。
到的边流量等于其容量。只有这样它才不会在残量⽹络中出现。

根据第⼀个条件，我们可以得知：没有流量从到之后⼜回到了。所以当前流量应该等于从到的边的流量之和，⽽根据第⼆个条件它⼜等于从到的边容量之和.⽽所有从到的边⼜构成⼀个割，其容量等于这些边的容量之和

这意味着我们找到⼀个流和⼀个割，使得前者的流量等于后者的容量。⽽根据前⾯的结论，最⼤流的流量不会超过这个割的容量，所以这个流⼀定是最⼤流！

同样的，最⼩割的容量也不会⼩于这个流的流量，所以这个割也⼀定是最⼩割。

⽽这就是⽅法最后的局⾯（由于会终⽌，所以它必定求出这样⼀个局⾯），由此我们得出结论：

FF是正确的，并且最大流等于最小割。 ~~（⽽最⼩割最⼤流定理还可以通过线性规划对偶定理证明）~~不⽤管这个⻤玩意。

证毕撒花.

其他最大流算法

窝就扔一个最大流板子的链接：[POJ]最大流板子

我们发现算法的复杂度太⾼（虽然⽹络流⼏乎没有跑到上界的情况，但复杂度还是在⼀定程度上代表了算法效率）

有⼀个显然的优化：

如果增⼴⼀次之后发现最短路没有变化，那么可以继续增⼴；直到从源点到汇点的增⼴路增⼤，才需要再跑⼀遍。

之后，我们取出那些可能在最短路上的边，即的那些边。显然这些边构成的图中没有环。我们只需要沿着这种边尽可能的增⼴即可。

我们利⽤增广。

有⼀个函数 int dfs(int x, int T, int maxflow) 表示从出发寻找到汇点的增广路，寻找到个流量为止，并相应的增广。其返回值为实际增广了多少（因为有可能找不到条增广路）

复杂度可以证明为。在某些特殊情况下（每个点要么仅有⼀条⼊边且容量为，要么仅有⼀条出边且容量为）其复杂度甚至能做到

Dinic 算法

算法的过程:

遍历残量网络，建立层次图；
在层次图上寻找任意一条增广路，进行增广，并将答案加上增广流量；
重复第步，直至层次图中不存在增广路，回到第步重新建立层次图；
直到层次图无法建立，则当前流量即为最大流量。

每次建立层次图后都可以进行多次增广，无法增广时重新建立层次图，此时的层次图不再包含之前进行增广后满载的边。无法建立层次图时，说明源点到汇点的任意一条简单路径中，都至少有一条边满载，这也在直观上验证了最小割最大流定理

伪代码

（假设是⼀个全局变量，表示汇点）邻接表存储，head[x] 表示从出发的第⼀条边，next[i] 表示的下⼀条边。最后⼀条边的 next 为

int dfs(int x, int T, int maxflow) {
	if (x == T) return maxflow;
	int ans = 0;
	for (int i = head[x];i != -1 && ans < maxflow; i = next[i]) {
		if (dis[to[i]] != dis[x] + 1 || ret[i] == 0) continue;
		int f = dfs(to[i], T, min(maxflow - ans, ret[i]))
		ret[i] -= f;
		ret[rev[i]] += f;
		ans += f;
	}
	return ans;
}

而的主过程如下:

int Dinic(int S, int T) {
	int ans = 0;
	while (bfs(S, T)) ans += dfs(S, T, 0x7fffffff);
	return ans;
}

这段代码⼗分简洁qwq

有一个常见的优化 — 当前弧优化

该优化基于一个显而易见的事实，每次建立层次图后，如果在某一次增广前，某个点有一条边增广过了，则这条边在当前的层次图中不会再用到了，即下一次这个点的时候直接可以从这条边的下一条边开始

SAP 算法

距离标号：

所谓距离标号，就是某个点到汇点的最少的弧的数量（即边权值为1时某个点到汇点的最短路径长度）

设点的标号为，那么如果将满足的弧叫做允许弧，且增广时只走允许弧

断层（本算法的优化思想）

数组表示距离标号为的点有多少个，如果到某一点没有符合距离标号的允许弧，我那么需要修改距离标号来找到增广路

如果重标号使得数组中原标号数目变为，则算法结束

我们学过毒瘤的算法，我们想想优化－如果能让每次寻找增广路时的时间复杂度降下来，那么就能提高算法效率了，使用 距离标号的最短增广路算法 就是这样的

Code:

/*qwq窝才不会给你代码*/

ISAP算法

原图存在两种子图，一个是残量网络，一个是允许弧组成的图

残量网络保证可增广，允许弧保证最短路（时间界较优）

所以，在寻找增广路的过程中，一直是在残量网络中沿着允许弧寻找。因此，允许弧应该是属于残量网络的，而非原图的

换句话说，我们沿着允许弧，走的是残量网络（而非原图）中的最短路径

当我们找到沿着残量网络找到一条增广路，增广后，残量网络肯定会变化（至少少了一条边），因此决定允许弧的数组要进行相应的更新（顺便提一句，的做法就是每次增广都重新计算数组）

然而，ISAP 「改进」的地方之一就是，其实没有必要马上更新数组。这是因为，去掉一条边只可能令路径变得更长，而如果增广之前的残量网络存在另一条最短路，并且在增广后的残量网络中仍存在，那么这条路径毫无疑问是最短的。所以，ISAP 的做法是继续增广，直到遇到死路，才执行操作

说到这里，大家应该都猜到了，操作的主要任务就是更新数组。那么怎么更新呢？

非常简单：假设是从节点找遍了邻接边也没找到允许弧的；再设一变量，令等于残量网络中的所有邻接点的数组的最小值，然后令等于即可。这是因为，进入环节说明残量网络中和已经不能通过（已过时）的允许弧相连

那么和实际上在残量网络中的最短路的长是多少呢？（这正是的定义！）

显然是残量网络中的所有邻接点和的距离加的最小情况。特殊情况是，残量网络中根本没有邻接点。

如果是这样，只需要把设为一个比较大的数即可，这会导致任何点到的边被排除到残量网络以外

（严格来说只要大于等于即可。由于最短路一定是无环的，因此任意路径长最大是）修改之后，只需要把正在研究的节点沿着刚才走的路退一步，然后继续搜索即可

int source;         // 源点
int sink;           // 汇点
int p[max_nodes];   // 可增广路上的上一条弧的编号
int num[max_nodes]; // 和 t 的最短距离等于 i 的节点数量
int cur[max_nodes]; // 当前弧下标
int d[max_nodes];   // 残量网络中节点 i 到汇点 t 的最短距离
bool visited[max_nodes];

// 预处理, 反向 BFS 构造 d 数组
bool bfs() {
    memset(visited, 0, sizeof(visited));
    queue<int> Q;
    Q.push(sink);
    visited[sink] = 1;
    d[sink] = 0;
    while (!Q.empty()) {
        int u = Q.front();
        Q.pop();
        for (iterator_t ix = G[u].begin(); ix != G[u].end(); ++ix) {
            Edge &e = edges[(*ix)^1];
            if (!visited[e.from] && e.capacity > e.flow) {
                visited[e.from] = true;
                d[e.from] = d[u] + 1;
                Q.push(e.from);
            }
        }
    }
    return visited[source];
}

// 增广
int augment() {
    int u = sink, df = __inf;
    // 从汇点到源点通过 p 追踪增广路径, df 为一路上最小的残量
    while (u != source) {
        Edge &e = edges[p[u]];
        df = min(df, e.capacity - e.flow);
        u = edges[p[u]].from;
    }
    u = sink;
    // 从汇点到源点更新流量
    while (u != source) {
        edges[p[u]].flow += df;
        edges[p[u]^1].flow -= df;
        u = edges[p[u]].from;
    }
    return df;
}

int max_flow() {
    int flow = 0;
    bfs();
    memset(num, 0, sizeof(num));
    for (int i = 0; i < num_nodes; i++) num[d[i]]++;
    int u = source;
    memset(cur, 0, sizeof(cur));
    while (d[source] < num_nodes) {
        if (u == sink) {
            flow += augment();
            u = source;
        }
        bool advanced = false;
        for (int i = cur[u]; i < G[u].size(); i++) { 
            Edge& e = edges[G[u][i]];
            if (e.capacity > e.flow && d[u] == d[e.to] + 1) {
                advanced = true;
                p[e.to] = G[u][i];
                cur[u] = i;
                u = e.to;
                break;
            }
        }
        if (!advanced) { // retreat
            int m = num_nodes - 1;
            for (iterator_t ix = G[u].begin(); ix != G[u].end(); ++ix)
                if (edges[*ix].capacity > edges[*ix].flow)
                    m = min(m, d[edges[*ix].to]);
            if (--num[d[u]] == 0) break; // gap 优化
            num[d[u] = m+1]++;
            cur[u] = 0;
            if (u != source)
                u = edges[p[u]].from;
        }
    }
    return flow;
}

最高标号预流推进(HLPP) 算法

算法思想

预流推进算法将每个点看做一个可以存储流的“水池”，其中存有流的点称为活动节点
对于每个非s或t的点，流入该点的流只可能有两个去向：流入汇点t，流回源点s;
预流推进算法从源点开始沿边向其它点推流，之后每次选一个活动节点通过推流，试图使其变得不活动。当所有节点都是不活动节点时，算法就结束了;
以上是传统预流推进算法的主要思想。而最高标号预流推进算法就是先预处理了一个距离标号h，通过堆或优先队列，没次选出h最大的点进行推流，以减少重复操作，降低了复杂度。

算法步骤

通过预处理出距离标号，即到达汇点的最短距离;
将从源点s出发的边设为满流，到达的点标记为活动节点并加入到优先队列中;
从优先队列中不断取出点进行推流操作，要求到达点的必须满足
若推流后中仍有余流，则进行重标号。将** 设为 **，再次加入优先队列并重复步骤 3.
当优先队列为空时，结束算法

算法复杂度：！！！

Code :

/* www.google.com */

CN001

2021-01-31 22:52:50

orzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorzorz

Album

2020-10-29 18:34:44

Herself32

2020-07-27 14:58:41

orz

Qingyu

2020-07-26 21:17:47

nkwnc

2020-07-26 16:21:43

orz